Distilling Task-Specific Knowledge from BERT into Simple Neural Networks

Author

• 저자:
  • Raphael Tang∗, Yao Lu∗, Linqing Liu∗, Lili Mou, Olga Vechtomova, and Jimmy Lin (University of Waterloo)

Who is an Author?

• ICASSP를 들고 있는 NLP 하던 분인 듯
• 보통은 문서분류쪽 많이 한듯

{: height=”50%” width=”50%”}

느낀점

• 아이디어는 간단함
• Data Augmentation을 넣은건 좋았음
• 그러나 성능이 좋아진게 Distillation 때문인지 Data Augmentation 때문인지를 정확히 다루지 않아서.. 이 부분이 이 논문의 최대 에러임

Abstract

• 요즘엔 BERT, ELMo, and GPT 같은 deep language representation model이 대세임
• 이러한 발전은 예전에 쓰던 shallower neural networks 를 안쓰게 만듬
• 본 논문에서는 lightweight neural network도 구조 변경, 추가 데이터, 추가 feature 없이도 아직 쓸만하다는걸 보여주려고함
• BERT에서 Knowledge distillation 해서 성능을 높여보려고함
• setence classification, sentence-pair task 등으로 테스트 할 것임
• ELMo보다 100배 적은 파리미터, 15배 빠른 추론속도로 비슷한 성능을 얻음

1. Introduction

• BERT등이 등장하면서 “first-generation” neural network가 잘 안쓰이게됨
• 본 논문에서는 간단하지만 효과적인 transfer 기법을 제안하고자함 (task-specific knowledge from BERT)
• single-layer BiLSTM을 사용할거고, BERT로부터 배울 것임
• 효율적인 knowledge transfer 를 위해선 데이터가 많이 필요하니, unlabled dataset으로부터 teacher output을 만들어서 student로 학습하게 할 것임

2. Related Work

• NLP에서 CNN, RNN 등이 발달됨
• 최근엔, ELMo(6가지 task SOTA 찍었음), BERT등이 등장함
• Model Compression:
  • local error-based method for pruning unimportant weights (LeCun et al. (1990))
  • Han et al. (2015) propose a simple compression pipeline, achieving 40 times reduction in model size without hurting accuracy. Unfortunately, these techniques induce irregular weight sparsity, which precludes highly optimized computation routines
  • quantizing neural networks (Wu et al., 2018); in the extreme, Courbariaux et al. (2016) propose binarized networks with both binary weights and binary activations
• 위에서 소개된 Model Compression과는 다르게 본 논문에서는 knowledge distillation appoach (Ba and Caruana, 2014; Hinton et al., 2015) 를 사용하고자함
• NLP에서 이미 이것에 대해 적용된 연구들이 있음(In the NLP literature, it has previously been used in neural machine translation (Kim and Rush, 2016) and language model- ing (Yu et al., 2018))

3. Our Approach

• First, teacher model과 student model을 선택 후 학습
• Second, 저자의 distillation procedure로 학습
  • logits-regression objective 사용
  • transfer dataset 구축

3.1 Model Architecture

• Teacher network : pretrained, fine-tuned BERT

  • feature vector ${ \boldsymbol{h} \in \mathbb{R}^{d} }$ 위에 우리가 사용할 classifier를 task에 맞게 추가해서 쓸것임
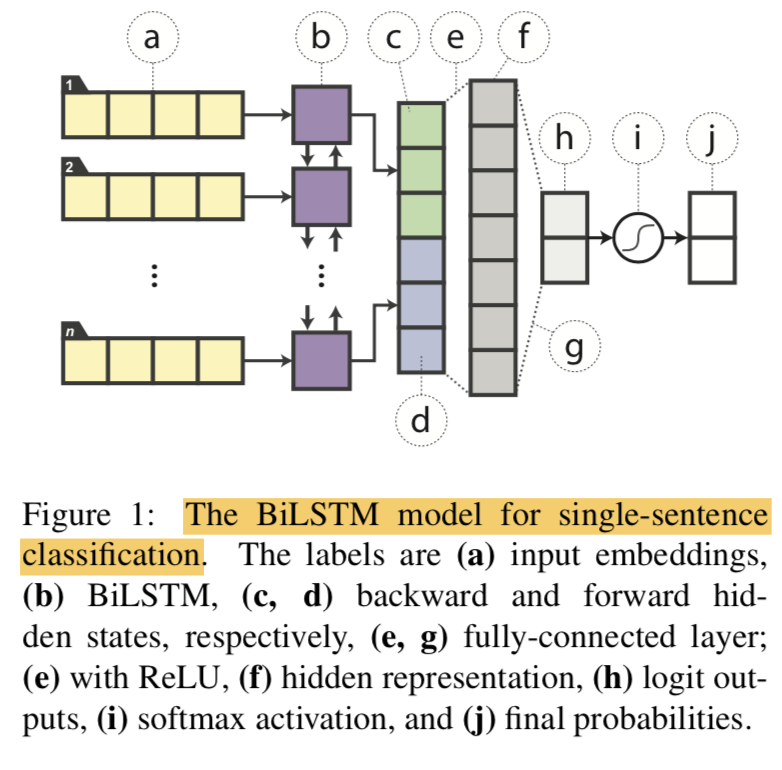
  • For single-sentence classification
    • 다음과 같이 softmax 추가해서 쓸 것임(${k}$ is the number of label) ${ \boldsymbol{y}^{(B)}=\operatorname{softmax}(W \boldsymbol{h}), \text { where } W \in \mathbb{R}^{k \times d} }$
  • For sentence-pair task
    • 두 문장에 대한 BERT features를 concat후 softmax layer에 넣는 방식으로 함
  • 학습시에는 BERT와 classifier에 대한 param을 둘다 업데이트하고 cross-entropy loss 사용함

• Student model: single-layer BiLSTM with a non-linear classifier

  • For classification

    • last step의 값을 concat 후 fc layer with ReLU 에 feed해서 softmax layer로 분류함
      {: height=”50%” width=”50%”}

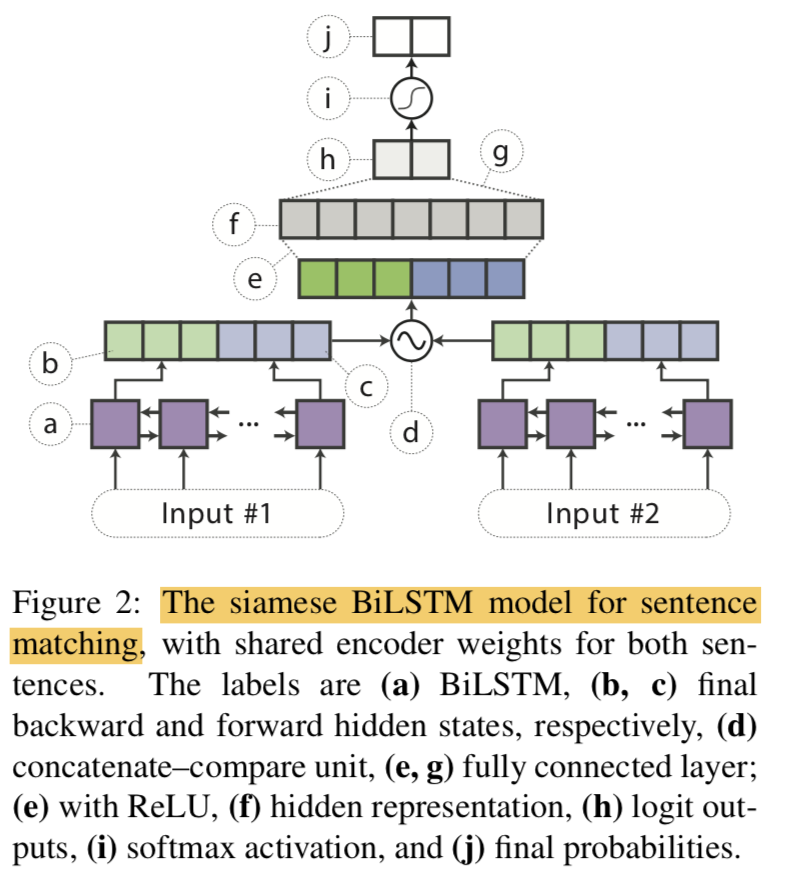
  • For Sentence-pair tasks

    • BiLSTM encoder weights를 share해서 siamese architecture로 사용 ${ \text { sentence vectors } \boldsymbol{h}{s 1} \text { and } \boldsymbol{h}{s 2} }$ 를 만들어냄
    • ${ \begin{array}{l}{f\left(\boldsymbol{h}{s 1}, \boldsymbol{h}{s 2}\right)=\left[\boldsymbol{h}{s 1}, \boldsymbol{h}{s 2}, \boldsymbol{h}{s 1} \odot\right.} {\left.\boldsymbol{h}{s 2},\left|\boldsymbol{h}{s 1}-\boldsymbol{h}{s 2}\right|\right], \text { where } \odot \text { denotes elementwise multiplication}}\end{array} }$
      {: height=”50%” width=”50%”}
    • attenion이나, layer norm 같은 스킬은 최대한 제외하고 BiLSTM의 representation Power에만 국한하는 설계를 함

3.2 Distillation Objective

• In addition to a one-hot predicted label, the teacher’s predicted probability is also important. In binary sentiment classifica- tion, for example, some sentences have a strong sentiment polarity, whereas others appear neutral.
• If we use only the teacher’s predicted one-hot label to train the student, we may lose valuable information about the prediction uncertainty.

$$
\widetilde{y}{i}=\operatorname{softmax}(\boldsymbol{z})=\frac{\exp \left{\boldsymbol{w}{i}^{\top} \boldsymbol{h}\right}}{\sum_{j} \exp \left{\boldsymbol{w}_{j}^{\top} \boldsymbol{h}\right}}
$$

$$
\begin{array}{l}{\text { where } w_{i} \text { denotes the } i^{\mathrm{th}} \text { row of softmax weight }} \ {W, \text { and } z \text { is equivalent to } \boldsymbol{w}^{\top} \boldsymbol{h} .}\end{array}
$$

• Training on logits makes learning easier for the student model since the relationship learned by the teacher model across all of the targets are equally emphasized (Ba and Caruana, 2014).

• student network’s logits과 teacher’s logits의 MSE로 distillation objective를 만듬 (Cross entropy등도 사용하능하나, 저자의 실험에서 MSE가 좀 더 결과가 좋았다고함)
  $$
  \mathcal{L}{\text {distill }}=\left|z^{(B)}-z^{(S)}\right|{2}^{2}
  $$

• 최종적인 Loss는 기존의 one-hot에 대한 CE loss와 distill Loss를 weighted sum해서 사용함 (${t}$는 one-hot label)
  $$
  \begin{array}{l}{\mathcal{L}=\alpha \cdot \mathcal{L}{\mathrm{CE}}+(1-\alpha) \cdot \mathcal{L}{\text {distill }}} \ {=-\alpha \sum_{i} t_{i} \log y_{i}^{(S)}-(1-\alpha)\left|z^{(B)}-z^{(S)}\right|_{2}^{2}}\end{array}
  $$

  • unlabeld data의 경우엔 teacher가 예측한걸 기준으로 사용함 ${ \begin{array}{l}{\text { i.e., } t_{i}=1 \text { if } i=\arg \max y^{(B)} \text { and } 0 \text { otherwise. }}\end{array} }$

3.3 Data Augmentation for Distillation

• 데이터 셋 작으면 티쳐한테 배울때 효과가 별로 없음
• 그렇기 때문에 데이터셋 키우기로함 (with pseudo-labels provided by the teacher)
• 하지만.. NLP에서의 Data augmentation은 Computer vision에 비해 어려움
  • CV는 비슷한 이미지들이 매우 많음 (CIFAR-10 is a subset of the 80 million tiny images dataset)
  • CV는 이미지 회전이나 노이즈 추가등.. 방법이 많음 (Second, it is possible to synthesize a near-natural image by rotating, adding noise, and other distortions)
    • NLP에서 이 방법 쓰면 not be fluent되기 때문에 쓸 수 없음 ㅠ
• 본 논문에서는 약간의 휴리스틱으로 task-agnostic data augmentation을 하려고함 (image distortion과 같진 않고, 비슷하다고 생각하면됨)
  • Masking:
    • ${p_{mask}}$ 의 확률로 랜덤하게 단어를 [MASK]로 바꿈
    • Intuitively, this rule helps to clarify the contribution of each word toward the label (각 단어의 contribution을 파악하는데 도움이 된다고 주장)
    • e.g., the teacher network produces less confident logits for “I [MASK] the comedy” than for “I loved the comedy.”
  • POS-guided word replacement:
    • ${p_{pos}}$ 의 확률로 단어를 같은 pos 태그를 갖는 다른 단어로 교체함 (허허 요상한 방법일세)
    • 이러한 룰은 semantic을 방해하기도 함 (This rule perturbs the semantics of each example, e.g., “What do pigs eat?” is different from “How do pigs eat?”)
  • n-gram sampling:
    • ${p_{ng}}$ 의 확률로 예시 문장에서 n-gram을 샘플링함 (n is randomly selected from {1,2,…,5})
    • n-gram 외의 단어는 드랍해버리는것과 비슷한 효과고 마스킹보다 더 공격적인 방법임 (This rule is conceptually equivalent to dropping out all other words in the example, which is a more aggressive form of masking)
• Data augmentation procedure:
  • training example ${w_{1}, …, w_{n}}$
  • 단어에 대해서 iteration 하면서 각 단어에 대해서 유니폼 분포로 확률을 계산함 ${ X_{i} \sim \text { UNIFORM }[0,1] \text { for each } w_{i} }$
  • ${ \text{if } X_{i}<p_{\text {mask }}, \text { we apply masking to } w_{i} }$
  • ${ \text{if } p_{\text {mask}}<X_{i}<p_{\text {mask }} + p_{\text {pos }}, \text { we apply POS-guided word replace to } w_{i} }$
  • masking과 POS-guided swapping은 mutuially exclusive하게 진행해서 한개가 적용되면 나머지는 적용안함
  • iteration이 끝나면, ${p_{ng}}$의 확률로 n-gram sampling을 synthetic example(위에서 만든 문장)에 적용하면 final synthetic example이 완성됨
  • 이러한 전체 프로세스를 한 문장당 $ n_{iter} $번 적용해서 총 $ n_{iter} $개의 문장을 만듬 (중복은 제거)
  • For sentence-pair datasets, we cycle through augmenting the first sentence only (holding the second fixed), the second sentence only (holding the first fixed), and both sentences.

4. Experimental Setup

• Teacher Network으로써의 BERT는 large 버전 사용
  • BERT fine-tuning 할 땐 Adam opt with lr {2,3,4,5} X ${10^{-5}}$ 적용
  • val set 기준 best model 선택
  • 여기선 data augmentation 안씀
• Student model 학습할 땐 data augmentation 사용
  • soft logit target을 사용한 모델을 ${\text BiLSTM_{SOFT}}$ 로 표기하겠음
  • 3.2 세션에서 weighted sum으로 기존 CE와 distillation Loss를 추가해서 만들었는데 ${\alpha = 0}$으로 셋팅해서 distillation objective만 사용한게 젤 잘나왔음

4.1 Datasets

• GLUE에서 3개 뽑아서 씀
  • SST-2: movie reviews for binary sentiment classification (positive vs. negative)
  • MNLI: to predict the relationship between a pair of sentences as one of entailment, neutrality, or contradiction
  • QQP: binary label of each question pair indicates redundancy

4.2 Hyperparameters

• Student Model
  • BiLSTM hidden: 150 or 300
  • RelLU activated hidden: 200 or 400
  • Optim: AdaDelta (lr: 1.0 ${\rho}$: 0.95)
  • Batch size: 50 (SST2), 256 (MNLI, QQP)
• Data Augmentation
  • ${p_{mask} = p_{pos} = 0.1 \text{ and } p_{ng} = 0.25}$
  • ${n_{iter}} = 20$ (SST), ${n_{iter}} = 10$ (MNLI, QQP)

4.3 Baseline Models

• BERT
• OpenAI GPT
• GLUE ELMo baselines

5. Results and Discussion

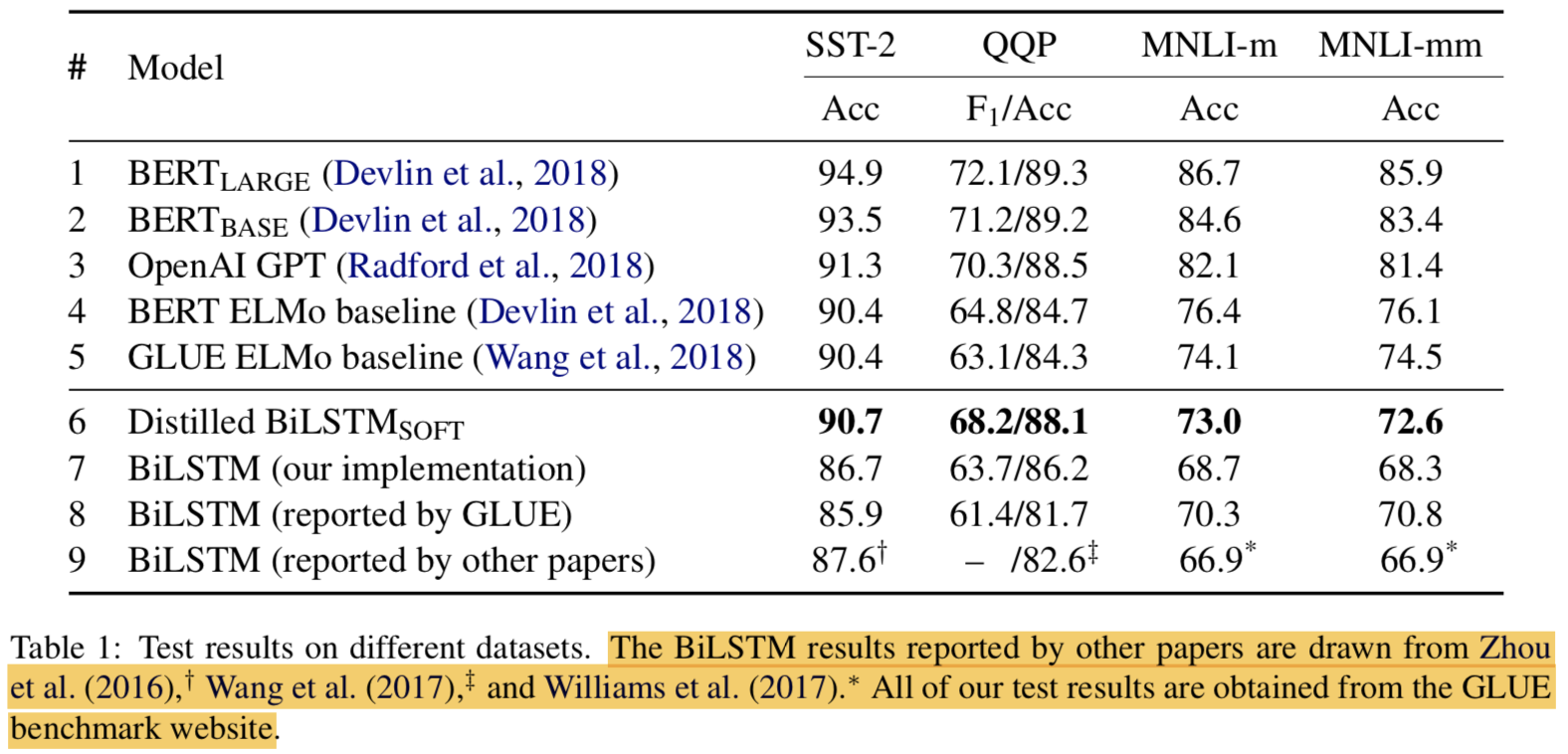
5.1 Model Quality

{: height=”50%” width=”50%”}

• our distillation approach of matching logits using the augmented training dataset, and achieve an absolute improvement of 1.9– 4.5 points against our base BiLSTM.
• data augmentation 없이 distillation한 것도 보여줘야.. 설득력이 더 있을텐데 음..

5.2 Inference Efficiency

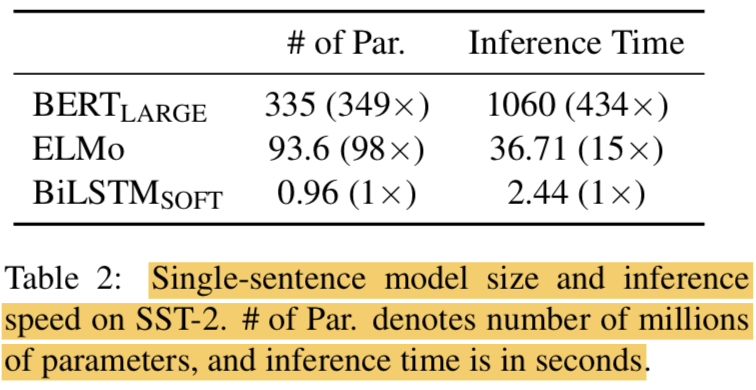
• On a single NVIDIA V100 GPU
• with a batch size of 512 on all 67350 sentences of the SST-2 training set
• our single-sentence model uses 98 and 349 times fewer parameters than ELMo and BERTLARGE, respectively
• 15 and 434 times faster

{: height=”50%” width=”50%”}

6. Conclusion and Future Work

• Explore distilling the knowledge from BERT into a simple BiLSTM-based model
• The distilled model achieves comparable results with ELMo, while using much fewer parameters and less inference time
• Future work로는 더 단순한 모델로 KD하거나 더 복잡한 모델로 KD하거나..(이거 넘 당연한 발상아닌가..)

Code

ref: https://github.com/qiangsiwei/bert_distill

Note:

• marp syntax 변경: https://marpit.marp.app/image-syntax