BERT-based Lexical Substitution

Author

• 논문 매우 많이 씀
• AAAI, ACL, ICLR 등 탑티어 컨퍼런스 논문냄
• 마소에서 인턴했고 2021 fall 박사과정 자리 구하는중 (아직 석사라는 뜻)
• 개인블로그 운영: https://michaelzhouwang.github.io/

{: height=”50%” width=”50%”} {: height=”30%” width=”30%”}

• 저자:
  • Wangchunshu Zhou, Ke Xu (Beihang University)
  • Tao Ge, Furu Wei, Ming Zhou (Microsoft Research Asia)

Abstract

• 이전 연구들은 lexical resources (e.g. WordNet)으로 부터 타겟의 동의어를 찾아서 substitute candidates를 얻어서 context를 보고 랭킹하는 식의 연구였음
• 이런 연구들은 두가지 한계점이 있음
  • 타겟 단어의 synonyms 사전에 없는 good substitute candidates를 찾아내지 못함
  • substitution이 문장의 global context에 주는 영향을 고려하지 못함
• 이 문제를 해결하기 위해, end-to-end BERT-based lexical substitution approach를 제안함
• annotated data or manually curated resources 없이 만든 substitute candidates 제안하고 검증함
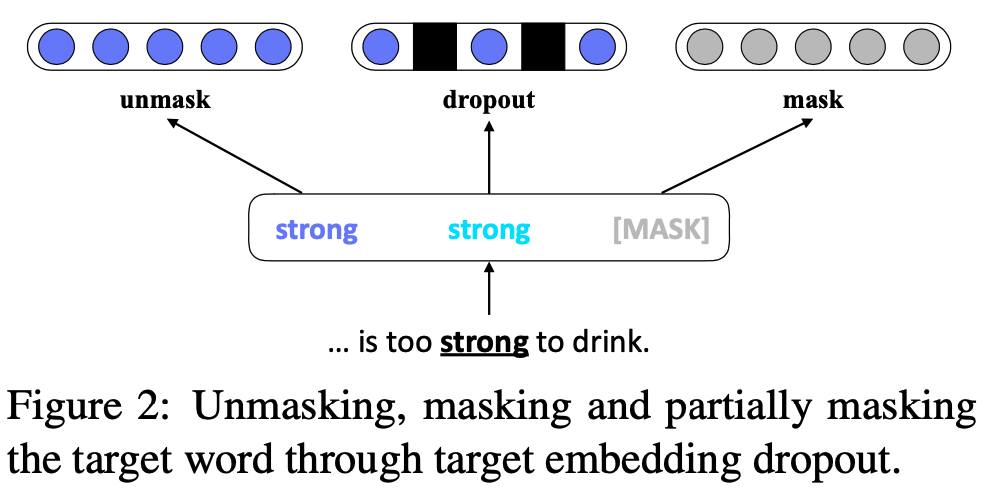
• target word’s embedding 에 dropout 적용해서 target word’s semantics and contexts for proposing substitute candidates를 고려할 수 있게함
• SOTA 찍음 (LS07, LS14 benchmark)

Introduction

• Lexical substitution은 문장의 의미를 바꾸지 않고 단어를 바꿔주는 task를 말함
• text simplication and paraphrase generation task와 비슷함
• 비슷한 단어 찾기와 맥락 의미 유지 두가지가 중요한데 대부분의 선행 연구는 첫번째 (동의어로 교체)에 초점이 맞춰짐

{: height=”40%” width=”40%”}

• 하지만 사전같은 리소스는 제한되어 있고, 바꾼 단어가 문장에 어떤 영향 주는지를 고려못함

BERT-based Lexical Substitution

Substitute Candidate Proposal

• 마스킹해버리면, 문장의 맥락상으론 맞지만 단어적으로는 틀린 단어 생성함
• 반대로 마스킹 안하면 거의 99.99% 의 확률로 original target word를 예측함
• 위 두개 방법의 trade-off를 고려해서 embedding dropout 하는걸 선택
• 문장이 있을때 문장에서 k 번째 단어를 나타내는 표현을 아래와 같이 한다고 할 때

$${\boldsymbol{x}=\left(x_{1}, \cdots, \underline{x}{k}, \cdots, x{L}\right)}$$

• proposal score $s_{p}\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)$ 는 $x_{k}$의 대체 단어로 $x_{k}^{\prime}$ 를 선택하는 점수임

$s_{p}\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)=\log \frac{P\left(x_{k}^{\prime} | \widetilde{\boldsymbol{x}}, k\right)}{1-P\left(x_{k} | \widetilde{\boldsymbol{x}}, k\right)}$

• $P\left(x_{k} | \boldsymbol{x}, k\right)$ 는 x라는 주어진 문장이 있을 때 k 번째 단어가 예측될 확률임
• $P\left(x_{k}^{\prime} | \widetilde{\boldsymbol{x}}, k\right)$ 이거는 k 번째 단어가 partially masked with embedding dropout인 경우임
• 분모 나눈건 origin word 의 확률을 빼줘서 normalize 해준 것임

{: height=”50%” width=”50%”}

python

token_prediction_scores = prediction_scores[문장내에서 변경할 토큰 위치, bert_token_index]            
origin_token_index = bert_token_ids[bert_token_index]

# 원래 토큰이 UNK면 그냥 UNK 확률 나오도록 살림
if origin_token_index != tokenizer.unk_token_id:
     token_prediction_scores[origin_token_index] = -1e9 # 원래 token이 다시 생성되지 않도록 마스킹
token_prediction_softmax_scores = F.softmax(token_prediction_scores)

cand_probs = token_prediction_softmax_scores
sum_probs = torch.sum(cand_probs)
proposal_scores = torch.log(cand_probs / sum_probs)

Substitute Candidate Validation

• 단어가 이상하게 선택되면 원래 문장과 의미가 달라지니, before after의 contextual representation을 비교하고자함
• BERT의 top four layer 의 representation을 concat해서 사용하겠음
• 단어가 교체된 문장은 다음과 같이 씀
  $$
  \boldsymbol{x}^{\prime}=\left(x_{1}, \cdots, x_{k}^{\prime}, \cdots, x_{L}\right)
  $$
• 이때 validation score는 다음과 같음
  $$
  s_{v}\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)=\operatorname{SIM}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime} ; k\right)
  $$
• SIM은 두 문장에 대한 BERT’s contextualized representation similarity 임
  $$
  \operatorname{Sim}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime} ; k\right)=\sum_{i}^{L} w_{i, k} \times \Lambda\left(\boldsymbol{h}\left(x_{i} | \boldsymbol{x}\right), \boldsymbol{h}\left(x_{i}^{\prime} | \boldsymbol{x}^{\prime}\right)\right)
  $$
• $\boldsymbol{h}\left(x_{i} | \boldsymbol{x}\right)$ 는 BERT의 i 번째 토큰에 대한 contextualized representation임
• $\Lambda(\boldsymbol{a}, \boldsymbol{b})$ 은 a, b 벡터의 cosine similarity임
• $w_{i, k}$ 은 i->k 방향의 모든 head에 대한 self-attention score의 평균임

Substitute Candidate Validation

• 음..오른쪽은 cosine으로 벡터간 유사도 보겠다는 거고 왼쪽은 attention으로 그것의 중요도를 대략 계산해보겠다는 거 같군
• 이렇게하면 예제에 나왔던 hot and touch 등의 단어는 validation (s_v) 점수가 낮게 나와서 랭킹에서 떨어지고 반면에 powerful 같은 단어는 높게 나와서 랭킹에서 올라감
• 최종적으로 다음과 같이 점수를 linear combination 해서 단어를 선택할 수 있음

$$
s\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)=s_{v}\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)+\alpha \times s_{p}\left(x_{k}^{\prime} | \boldsymbol{x}, k\right)
$$

python

input_ids = torch.tensor(token_ids_list, device=device)
 with torch.no_grad():
     last_hidden_states, pooler_output, hidden_states, attentions = bert_model(input_ids)

 num_of_top_hidden_use = 4 # top 4 layer
 stacked_token_attentions = torch.stack([ attention[0].mean(axis=[0]) for attention in attentions[-num_of_top_hidden_use:] ])    

 # layer 별로도 평균
 token_attentions = torch.mean(stacked_token_attentions, axis=0)

 # hidden layer 'num_of_top_hidden_use' 개수만큼 합치자
 subj_h = torch.cat([ hidden[0] for hidden in hidden_states[-num_of_top_hidden_use:] ], dim=-1)

 list_of_cand_h = []
 for i in range(1, len(token_ids_list)):
     list_of_cand_h.append(torch.cat([ hidden[i] for hidden in hidden_states[-num_of_top_hidden_use:] ], dim=-1))

 output = []
 for cand_i, cand_h in enumerate(list_of_cand_h):
     cos_sims = cos(subj_h, cand_h)    
     change_token_index = list_of_change_token_index[cand_i]
     w_i_to_k = token_attentions[:,change_token_index] # 논문대로 i to k attention만 남기기
     weighted_cos_sims = w_i_to_k * cos_sims    
     validation_score = torch.sum(weighted_cos_sims) # cls, sep 제거안함
     output.append(validation_score.item())

Experiments

Experimental Setting

• target word’s embedding dropout ratio: 0.3
• weight alpha: 0.01
• num candidates: 50

Experimental Results

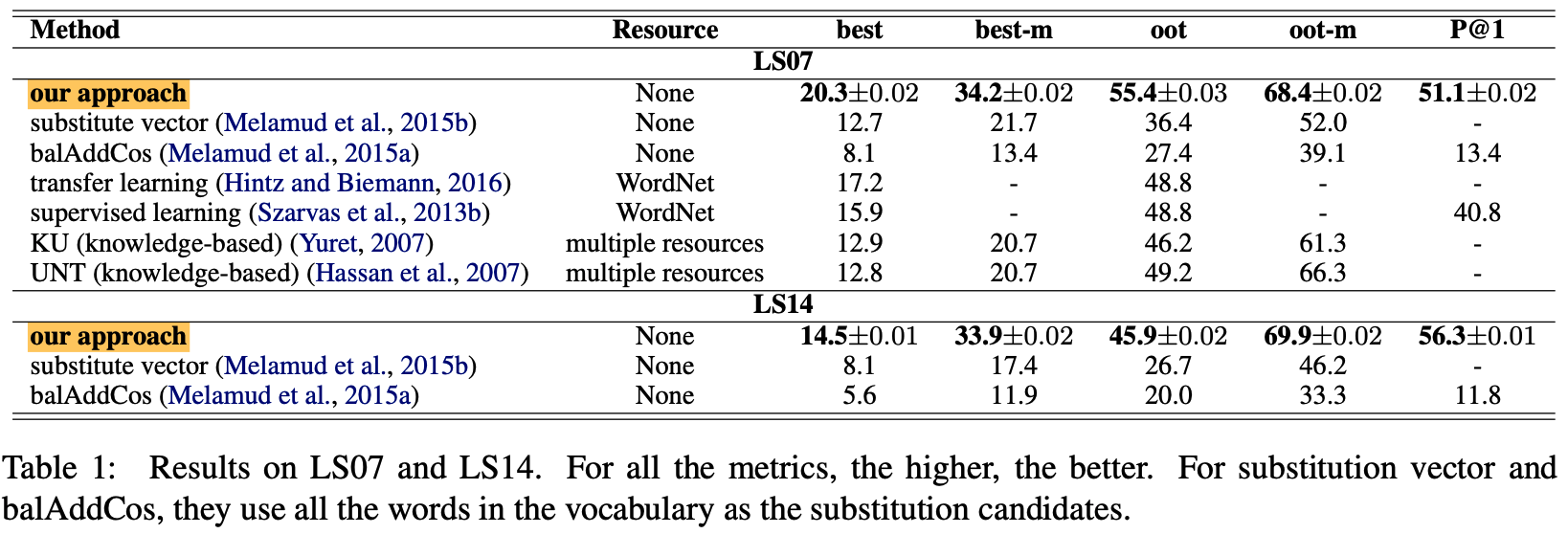
• original BERT는 기존 sota를 이길 수 없음 (Table 2 참고)
• embedding dropout 후 SOTA 먹음
• GAP score 라는 걸로 평가함 (MAP의 변형임)
  {: height=”50%” width=”50%”}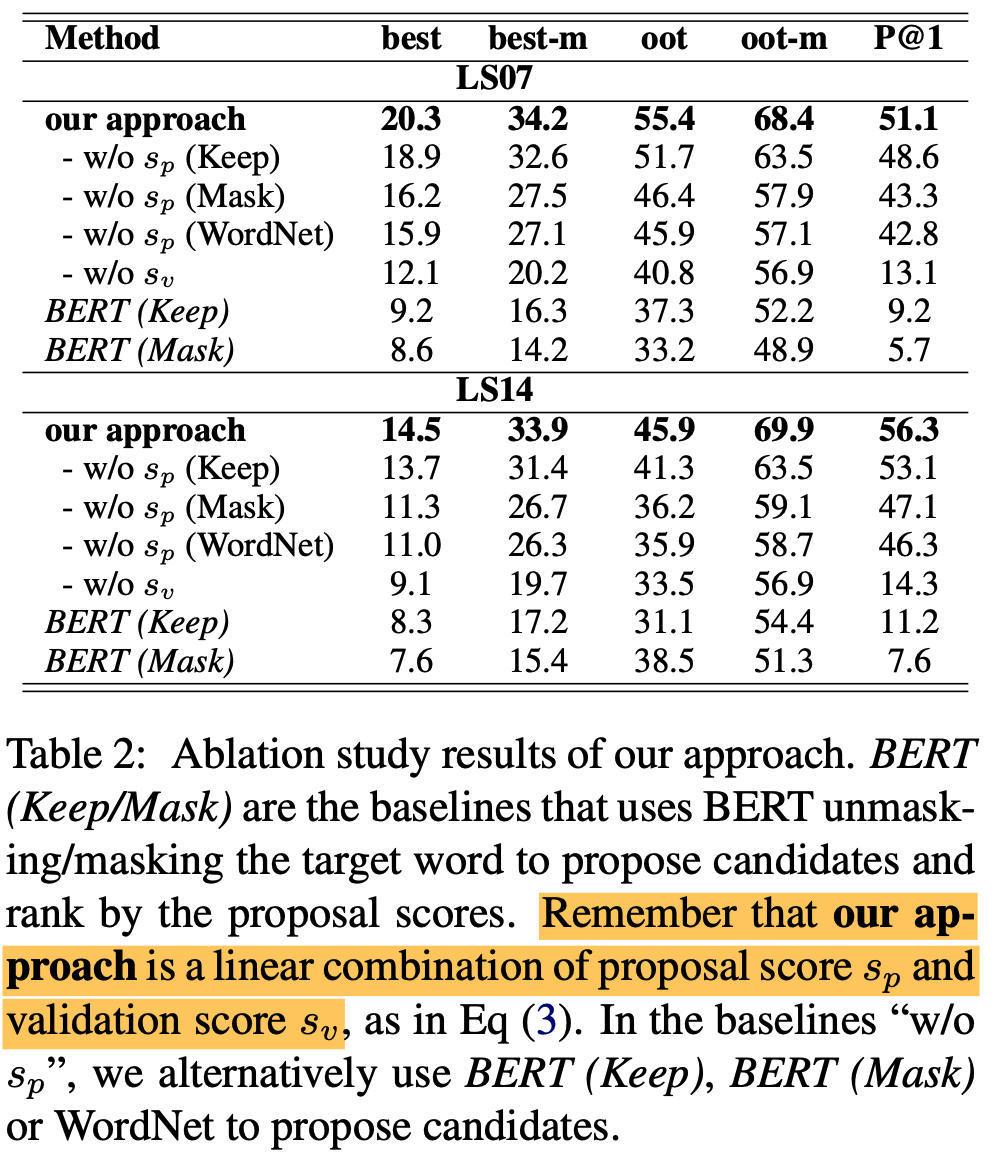
  {: height=”50%” width=”50%”}
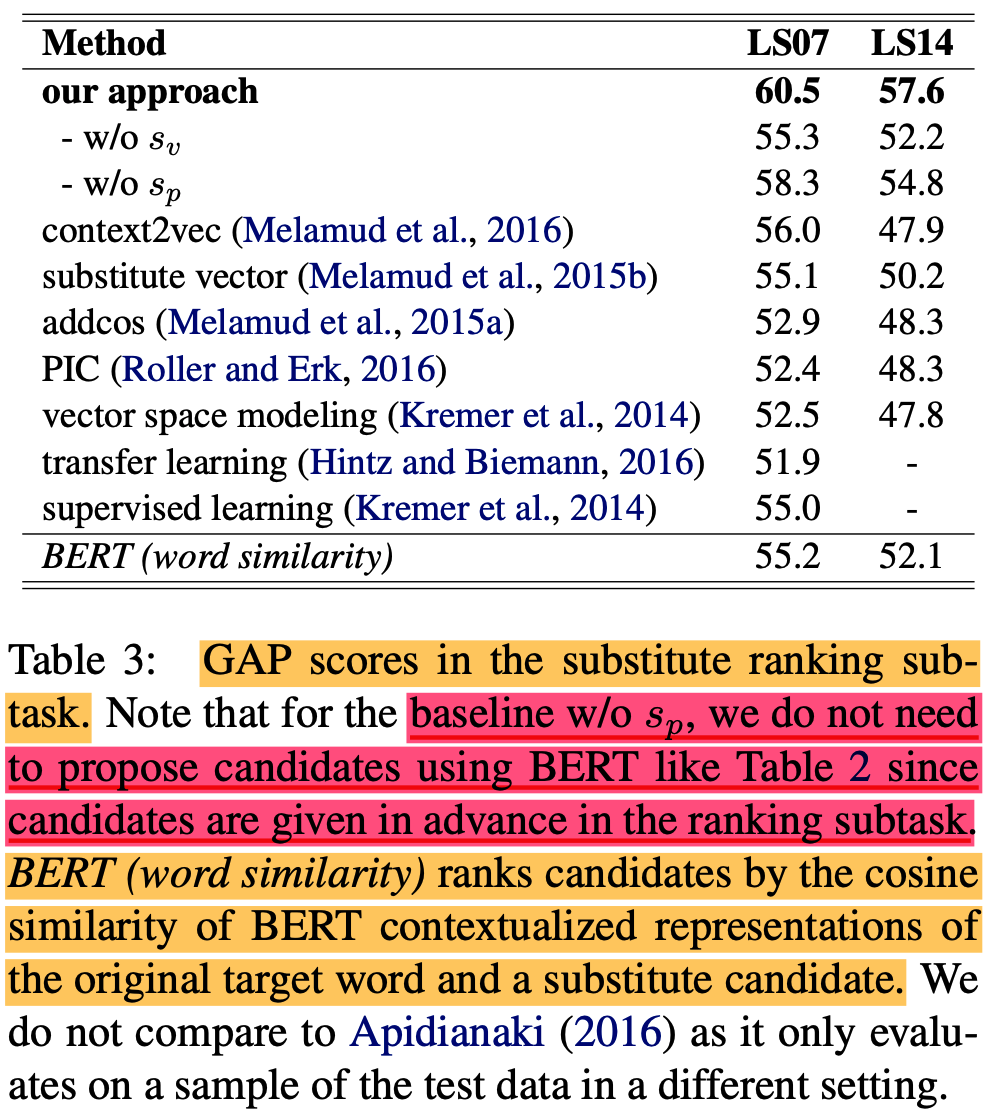  {: height=”50%” width=”50%”}

Conclusion

• annotated data and manually curated resources 없이도 결과 잘 나옴
• end-to-end 모델이고 sota임