게시 됨 업데이트 됨cslog21분안에 읽기 (약 3222 단어)

ML Basic - 머신러닝과 확률

Prior & Posterior

  • 사전 확률(prior probability):

    • 관측자가 관측을 하기 전에 시스템 또는 모델에 대해 가지고 있는 선험적 확률. 예를 들어, 남여의 구성비를 나타내는 p(남자), p(여자) 등이 사전확률에 해당한다.
    • 특정 사상이 일어나기 전의 확률을 뜻한다.
    • 선험적 확률은 베이즈 추론에서 관측자가 관측을 하기 전에 가지고 있는 확률 분포를 의미한다.
    • ex) 동전을 던져서 앞면이 나올 확률은 1/2, 특이한 동전은 1/3이다.
    • 사전 확률은 일반적으로 실험하는 대상에 대해 잘 알고 있는 전문가가 선택하거나(informative prior), 혹은 전문적인 정보가 없는 무정보적 분포(uninformative prior)로 주어진다.

  • 사후 확률(Posterior):

    • 사건이 발생한 후(관측이 진행된 후) 그 사건이 특정 모델에서 발생했을 확률
    • 사건 발생 후에 어떤 원인으로부터 일어난 것이라고 생각되어지는 확률
    • 조건부 확률을 통해 사후 확률을 표현할 수 있음
    • 사전 확률과 가능도(likelihood)가 주어졌을 때, 관측자는 관측값을 얻은 다음 베이즈 정리에 의해 사후 확률을 얻을 수 있음
    • ex) 물건이 불량품이 생산되었을때 A공장에서 생산되었을 확률
    • $posterior = {likelihood \times prior \over evidence}$

MLE & MAP 예시

  • MLE(Maximum Likelihood Estimation) 방법

    • MLE 방법은 남자에게서 그러한 머리카락이 나올 확률 p(z|남)과 여자에게서 그러한 머리카락이 나올 확률 p(z|여)을 비교해서 가장 확률이 큰, 즉 likelihood가 가장 큰 클래스(성별)를 선택하는 방법

  • MAP(Maximum A Posteriori) 방법

    • MAP 방법은 z라는 머리카락이 발견되었는데 그것이 남자것일 확률 p(남|z), 그것이 여자것일 확률 p(여|z)를 비교해서 둘 중 큰 값을 갖는 클래스(성별)를 선택하는 방법
    • 즉, 사후확률(posterior prabability)를 최대화시키는 방법으로서 MAP에서 사후확률을 계산할 때 베이즈 정리가 이용됨

  • 즉 MLE는 남자인지 여자인지를 미리 정해놓고 시작해서 비교하는거고 MAP는 남자인지 여자인지를 모르는 상태에서 그것이 정해지는 확률까지도 고려해서 비교하는 것임

  • MAP가 그래서 특정 경우가 정해지는 것에 대한 사전확률을 고려한다고 하는 것임

Maximum Likelihood Estimation (MLE)

Maximum a Posteriori Estimation (MAP)

MLE vs MAP

{: height=”50%” width=”50%”}

최대 사후 확률에 대응하는 모수(Parameter)는 최대우도(MLE)와 마찬가지로 모수의 점 추정으로 사용할 수 있지만, 최대우도에서는 어떤 사건이 일어날 확률을 가장 높이는 모수를 찾는 것에 비해, 최대 사후 확률 모수는 모수의 사전 확률(Prior)과 결합된 확률을 고려한다는 점이 다르다.

  • 한줄 정리: MAP는 MLE에 비해서 Params(성비로 생각하면 편함)로 인해 발생할 사건의 사전확률(성비를 생각하면 편함)을 고려함!

  • MLE보단 MAP 방법이 정확하지만 대부분 Params의 사전확률(성비)을 모르는 경우가 많기 때문에 MLE를 사용함

  • Params의 사전 확률을 왜 알기 어렵나?? (Blog Reference)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
영상에서 피부색을 검출하는 문제는 결국, 영상의 각 픽셀이 피부색인지 아닌지 여부를 결정하는 classification 문제로 볼 수 있다.

피부색 검출을 위해서는 먼저 샘플 영상들을 열심히 수집해서 피부색 DB와 일반 색상 DB를 구성해야 한다. 
DB구성이 끝나면 이제 입력 영상의 각 픽셀값이 피부색인지 여부를 베이지언 방법으로 판단해 보기로 하자. 
입력 픽셀값이 z라 하면 p(z|피부색)은 피부색 DB에 있는 데이터들 중에서 z와 같은 색을 가진 데이터의 비율을 세면 된다. 
또한 p(z|일반색)은 일반색 DB에 있는 데이터들 중에서 z와 같은 색을 가진 데이터의 비율이다.

만일 ML로 피부색 검출을 한다면 p(z|피부색)과 p(z|일반색)을 비교해서 확률이 큰 값을 선택하면 될 것이다.

그런데, 이 문제를 MAP로 풀면 어떻게 될까? 
수집된 DB에 있는 데이터의 개수를 이용하여 
p(피부색) = |피부색DB|/(|피부색DB|+|일반색DB|), p(일반색) = |일반색DB|/(|피부색DB|+|일반색DB|)
라 놓고 MAP를 적용하면 되는 것일까?

대답은 NO!

p(피부색)은 세상에 존재하는 모든 이미지 색상들 중에서 피부색이 얼마나 되느냐를 나타내는 말이다. 
따라서, 자신이 수집한 피부색 DB와 일반색 DB의 크기만을 가지고 이 확률을 추정하는 것은 무리가 있다. 
오히려 일반색 DB에 있는 데이터들 중에서 피부색 DB에 있는 색과 같은 색을 갖는 데이터들의 비율을 p(피부색)이라 잡는 것이 보다 합리적일 것이다.

이와 같이 prior 확률 p(x)를 구하는 것은 쉬운 문제가 아니기 때문에 현실적으로는 MAP 대신 ML이 사용되는 경우도 많다.

  • 여기까지 안가도, 정확한 성비를 구하려면 모든 인구의 인원과 성별별로 인원을 구해야되니.. prior를 구하기 어려울 수 있다 하겠다.

  • Q) MAP나 이런게 Neural Net이나 이런 부분에선 어떻게 적용될 수 있는걸까? DL에서는 거의 MLE 쓰는거 같은데..?! 아무래도 이런건 정보이론을 좀 더 공부해야 할듯..

Notation

  • P(A, B): A,B의 Joint Prob

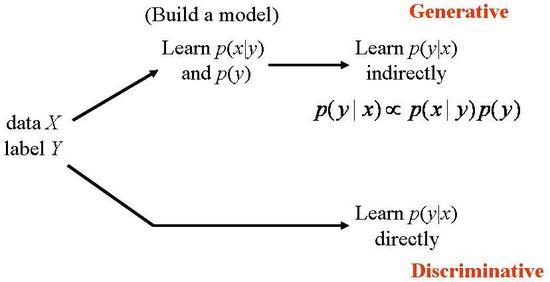
Generative vs Discriminative

  • Generative:

    • Joint Prob: P(X, C) = P(X|C)P(C) // Bayes rule로 해결
      • 여러개의 그래프
      • 후보 토픽을 정하고 각 토픽의 분포에 따라 단어가 생성될 확률 계산
    • 평균 분산만 두개 구하면 N 분포 쓸수있고 대부분을 N 으로 가정하니까 예전에 데이터 적을땐 Discriminative로 feature만드는것보다 Generative로 분포 가정해서 사용했음
    • multi feature를 보기 힘듬..!

  • Discriminative:

    • Conditional Prob: P(C|X)
      • 한개의 그래프
    • feature등을 통해 class 추측

gen_vs_dis

Probability Theory vs Decision Theory vs Information Theory

  • Probability Theory:
  • Decision Theory:
  • Information Theory:
    • 획득가능한 정보량 = 불확실성
    • 비트로 처음에 연구됨 (2진수)
    • 담아야되는 정보량(로그 밑은 2임) n = -logP(x) = log(1/P(x))
      • 2진수가 표현가능한 정보량
    • 정보량이란 그 사상에 대해 모르는 정도에 대한 양

etc

  • Generative: HMM (전이확률 + 생성확률)

  • Discriminative: NB (각 feature는 독립으로 보자~)

  • Maximum Entropy: 본 데이터에 대한 확률(feature function(있으면 1 없으면 0으로 나타내고 실제 중요도는 그 앞에 곱해지는 가중치인 alpha값을 학습해서 정함) + 유니폼(엔트로피 최대)

  • MEMM: HMM과 비슷하지만 전이확률 대신 엔트로피로..?! 하지만 Label bias라는 문제가 있음 (길이 없으면 가지마라 라는.. 데이터 없으면 방해될 수 있음)

  • CRF: MEMM 저자가 1년 후 만들어낸 모델임.. Linear Chain CRF가 우리가 아는 CRF임

    • 원래 CRF는 어떠한 클릭(사이클 만족시키지 않는..어떤 조건이 있는데 그걸 만족시키면 클릭임)도 자질로 쓸 수 있다
    • 이전 상태의 feature function의 가중치도 상태에 따라 달라지고.. 전이 확률이 너무 Label bias 문제를 만드니 이걸 하나의 feature로 보면서 영향을 줄여보겠다는게 CRF의 컨셉이라고 할 수 있음

  • Structured SVM:

    • SVM은 원래 분류만하는데 SVM으로 sequence 라벨링 문제 해결하려고 할때 씀

Examples

  • 가정: 어느 공장이 있다고 가정하자. 공장은 3개가 있다.
  • 목표: $P(Y \mid X)$ ; 불량품이 생산되었을때 어떤 공장에서 생산되었는지에 대한 확률을 구하는 것
  • 노테이션:
    • A, B, C: 공장
    • X: 불량인 경우의 클래스
  • 조건:
    • $P(A)$ = 35% : A 공장에서 물건을 생산할 확률이 35%임
      • $P(A \cap X)$ = 1% : A 공장에서 생산하고 불량인 확률
    • $P(B)$ = 20% : B 공장에서 물건을 생산할 확률이 20%임
      • $P(B \cap X)$ = 1.3% : B 공장에서 생산하고 불량인 확률
    • $P(C)$ = 45% : C 공장에서 물건을 생산할 확률이 45%임
      • $P(C \cap X)$ = 2% : C 공장에서 생산하고 불량인 확률

이번엔 $P(A \mid X)$에 대한 값을 구해보도록 하겠다.

$P(A \mid X)$ = ${P(X \mid A) P(A) \over P(X)}$ = ${P(X \cap A) \over P(A)} P(A) \over P(X)$ = $P(X \cap A) \over P(X)$

와 같이 정리할 수 있다. 이때, $P(A)$ = 35% 지만 쓸일이 없고, $P(X)$ = (불량 개수 / 전체 생산수) 로 구할 수 있거나 marginal prob로 구할수 있었던것 같다. 아무튼 남은건 $P(X \cap A)$인데, 이 친구는 독립인경우에 $P(X) * P(A)$로 바꿔서 쓸수있지만 (그렇게 되면 결국 $P(A|B)=P(A)$이다) 여기선 독립이 아니기 때문에 단순하게 곱하기로 하면 안된다. $P(X \cap A)$ 는 A 공장에서 생산했고 불량인 제품의 확률을 사용해야하므로 위에 정의된 1%를 써야한다.
결과적으로 다음과 같다.
$P(A \mid X)$ = $P(X \mid A) P(A) \over P(X)$ = ${P(X \cap A) \over P(A)} P(A) \over P(X)$ = $P(X \cap A) \over P(X)$ = $0.01 \over P(X)$

A를 클래스로 해석해서 그렇지 파라미터등으로 해석해서 모델을 찾는걸로 바꾼다면, 위의 값을 Maximize하는것이 중요하기 때문에, $P(X)$ 의 값은 사실상 고려하지 않아도 된다. 저 형태의 값의 크기가 가장 크게 나오는 theta만 찾으면 된다.

기타

  1. Forward
  2. Viterbi(Dynamic으로 해결하는데, forwad일때 이전 상태에서 최대값의 확률을 갖는 path를 저장해놓고 나중에 backward할때 다시 계산하지 않고 저장한 path를 사용하면서 해결하는 방식음)
    • N-Best하면 계산량 너무 많으니 계산량 줄이기 위해 beam search 같은거 하는 것..!
  3. Shortest path

loss function 정리

Reference

ML Basic - 머신러닝과 확률

https://eagle705.github.io/2019-09-11-MLbasic/

Author

Joosung Yoon

Posted on

2019-09-11

Updated on

2022-08-27

Licensed under

#

댓글

팔로우

카테고리

아카이브

태그

ML2
docker1
drone1
grpc1
linux1
nlp43
nlp, kb2
search1
web1
생각정리1

광고

최근 글

×